СИМПЛИЦИАЛЬНО-МОДУЛЬНЫЙ ДИЗАЙН
КАК ОСНОВА МОДЕЛИРОВАНИЯ МЕТАЛЛИЧЕСКИХ КЛАСТЕРОВ
(АЛГОРИТМЫ СБОРКИ)
ОСНОВНЫЕ РАБОТЫ
Тытик Д. Л. Симплициально-модульный дизайн Н.А. Бульенкова как основа моделирования металлических кластеров // Журнал физической химии. 2023. том 97. № 1. С. 26–36.
Бульёнков Н.А., Тытик Д.Л. // Известия РАН, сер. химич. 2001. Т. 50. № 1. С.1.
Tran N.T., Powell D.R., Dahl L.F. // Angew. Chem. Int. Ed. 2000. No. 39. P. 4121.
Martin T.P. // Solid State Ionics. 2000. No. 131. P. 3.
de Heer W.A. // Rev. of Modern Physics. 1993. V. 65. No. 3. P.611.
Knight W.D., Clemenger K., de Heer W.A. et al. // Phys. Rev. Lett. 1984. V. 52. No. 24. P. 2141.
Barker J. The geometries of soft-sphere packings. Journal de Physique Colloques, 1977, 38 (C2), pp.C2-37-C2-45.
МОДЕЛИРОВАНИЕ СТРУКТУРЫ КЛАСТЕРОВ
Моделирование структуры кластеров обусловлено отсутствием прямых методов определения положения (координат) атомов. Это обстоятельство в некоторой степени компенсируется данными, например, масс-спектрометрии, в которых регистрируется набор максимумов интенсивности, отвечающий определенному числу атомов в ряду стабильных кластеров (магические числа атомов). В [1, 2] показано, что если в основу ряда кластеров положить минимальное «ядро» из атомов, размещенных в вершинах правильных многогранников (тела Платона и Архимеда), то каждое магическое число соответствует завершению очередного слоя атомов по модели плотной упаковки. Это относится, например, к кластерам ряда Кини с магическими числами атомов: 13, 55, 147, 309, 561… [2]. С развитием нанотехнологии появлялись все новые данные о регистрации стабильных наночастиц разных металлов с другими магическими числами [3, 4]. Стало ясно, что для объяснения их строения не достаточно использовать только модель плотной упаковки и послойного заполнения атомами очередного внешнего слоя наночастицы. Н.А.Бульенков показал, что проблема моделирования строения апериодических структур, к которым относятся кластеры, может быть решена с применением локального подхода [5, 6].
Библиография к материалу
1. Chini P. // Gazzetta Chimica Italiana. 1979. No 109. P. 225.
2. Teo B.K., Sloane N.J.A. // Inorg.Chem. 1985. No 24. P. 4545.
3. de Heer W.A. // Rew.of Modern Physics. 1993. V. 65. No. 3. P.611.
4. Knight W.D., Clemenger K., deHeer W.A. et al. //Phys.Rev.Lett. 1984. V. 52. No. 24. P. 2141.
5. Бульенков Н.А. // «Вестник Нижегородского Университета им. Н.И. Лобачевского» сер.«Физика твердого тела». 1998. вып.1. С.19.
6. Делоне Б.Н., Долбилин Н.П., Штогрин М.И., Галиулин Р.В. // Докл. АН СССР. 1976. Т. 227, № 1. С. 19.
ПРЕДСТАВЛЕНЫ МОДЕЛИ КЛАСТЕРОВ МЕТАЛЛОВ, ПРЕДЛОЖЕННЫЕ Н.А. БУЛЬЕНКОВЫМ
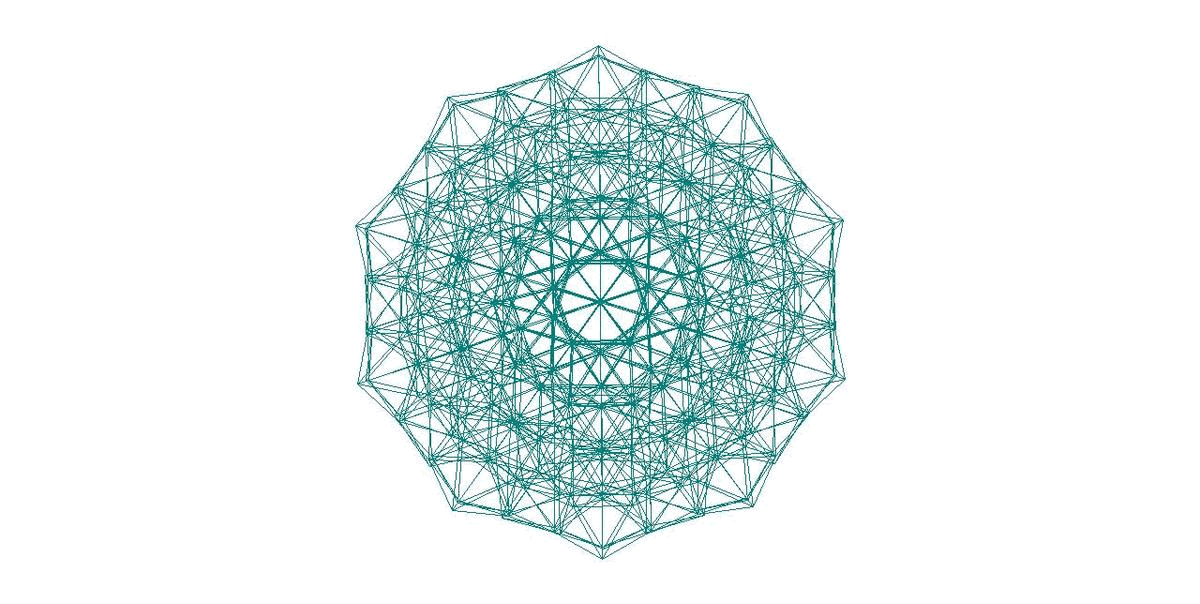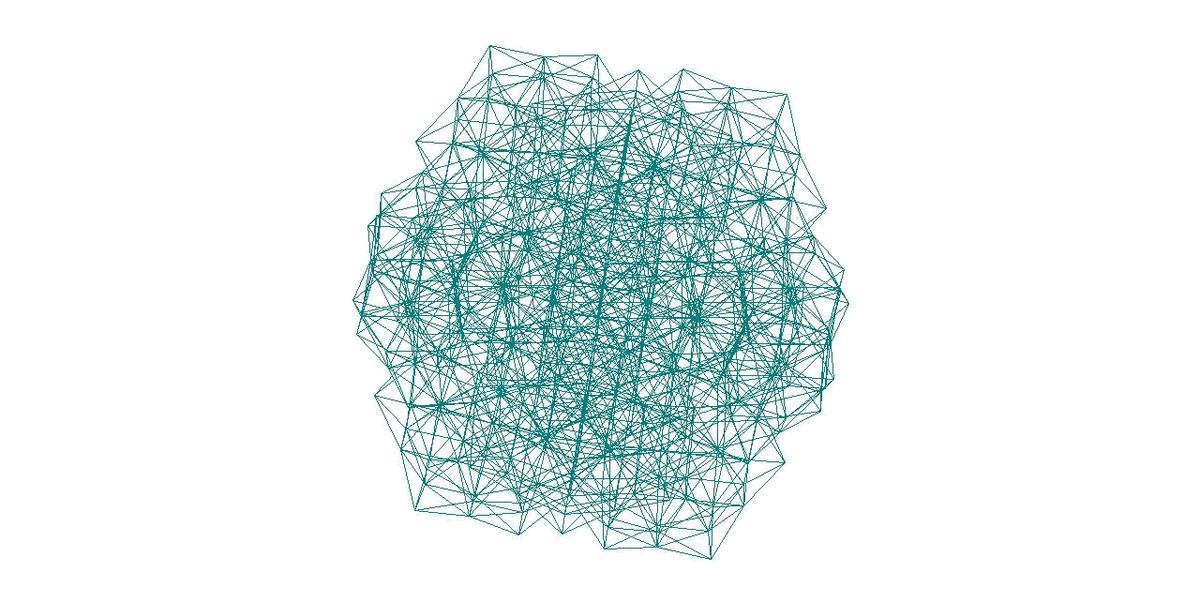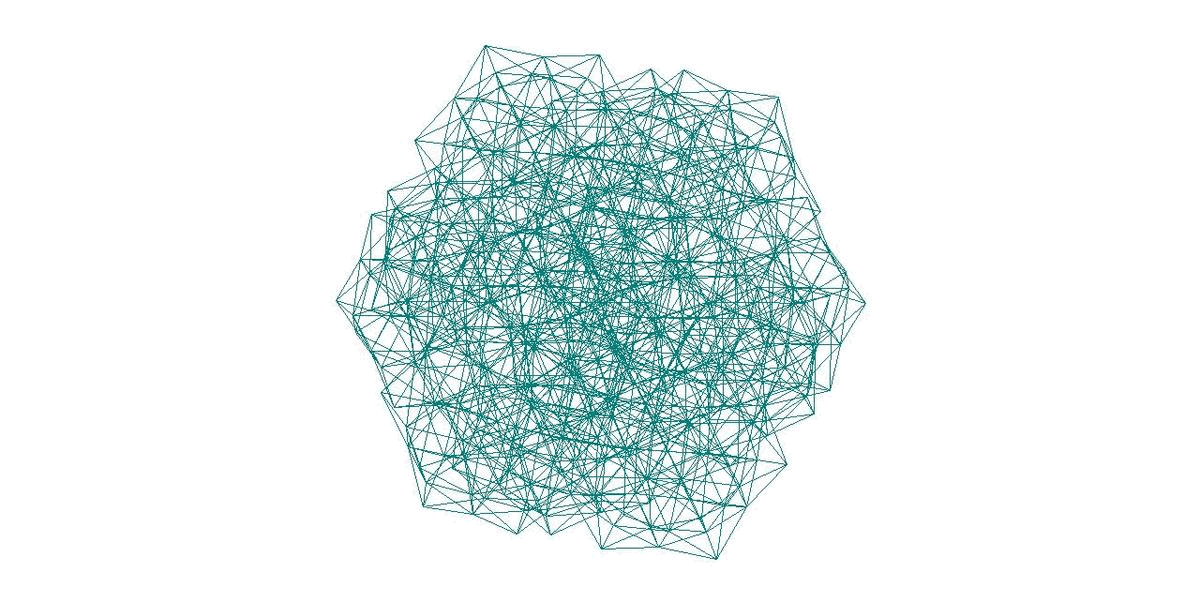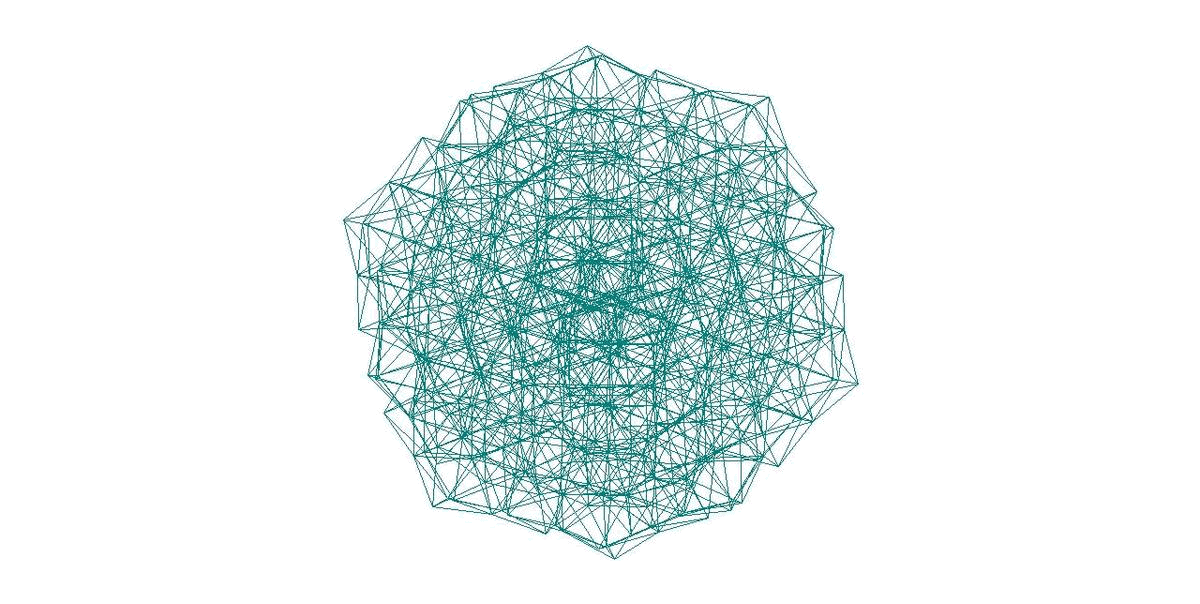
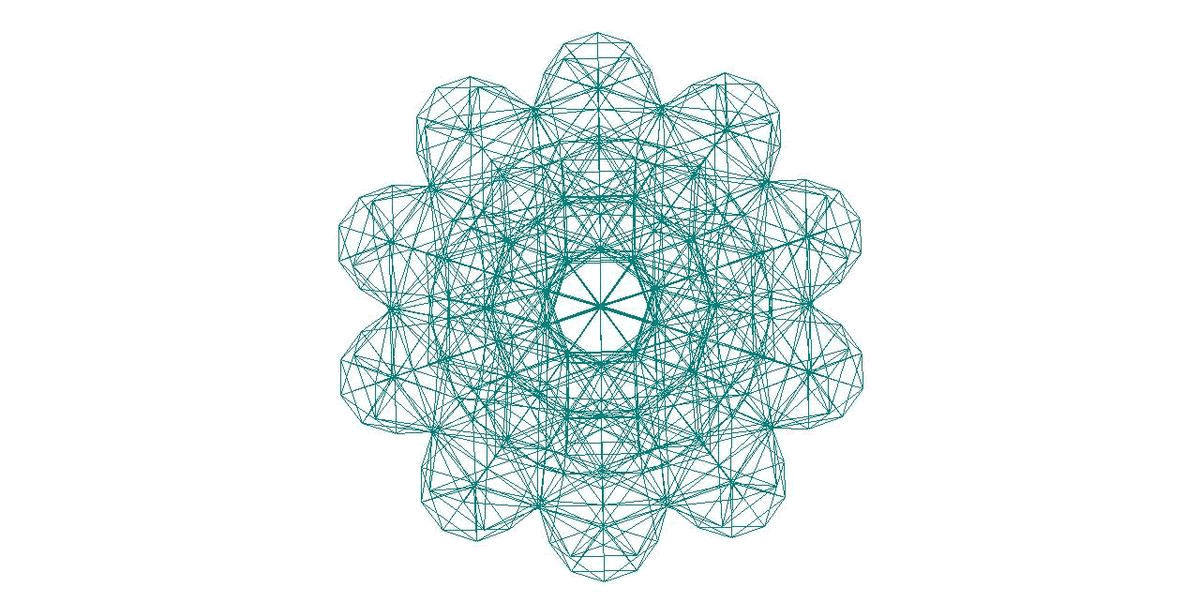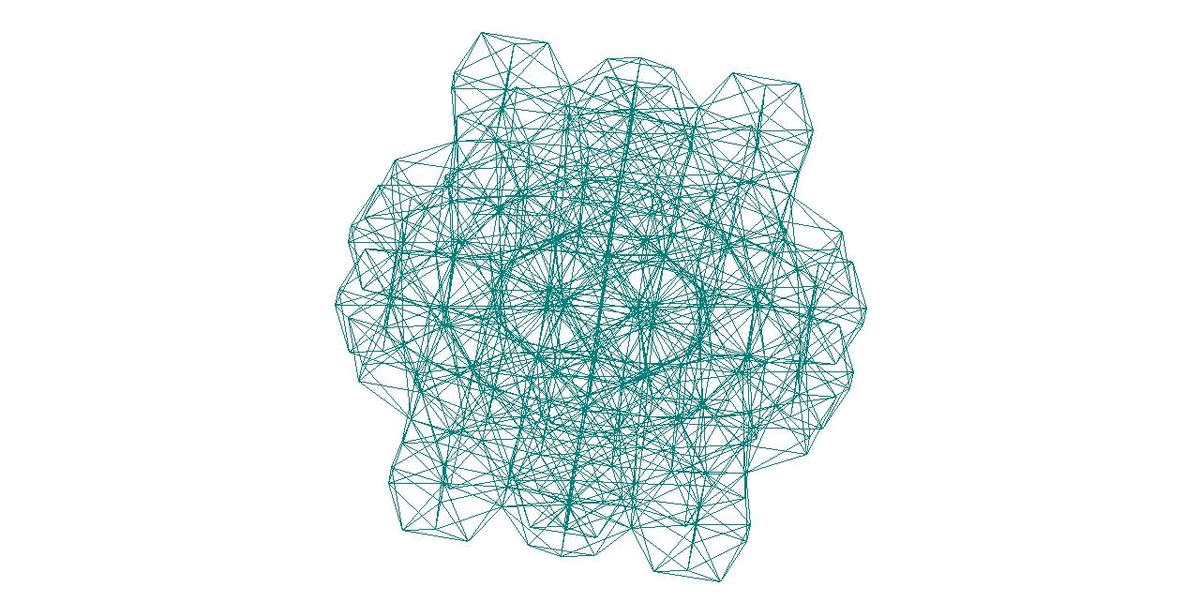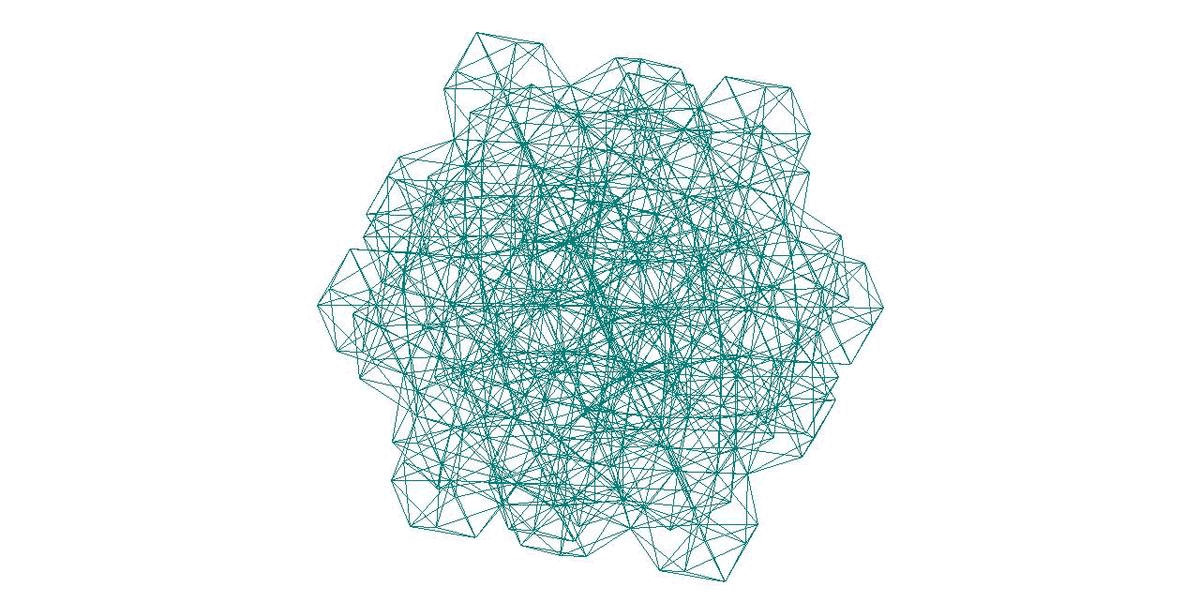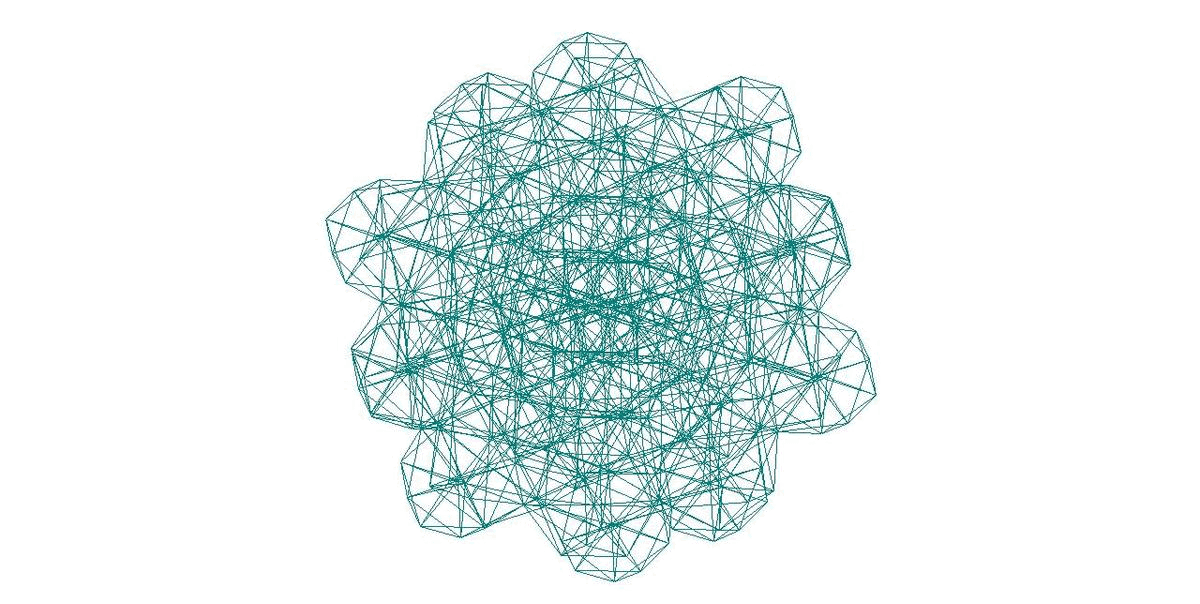
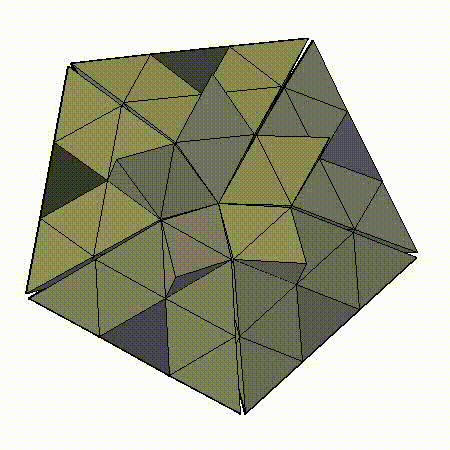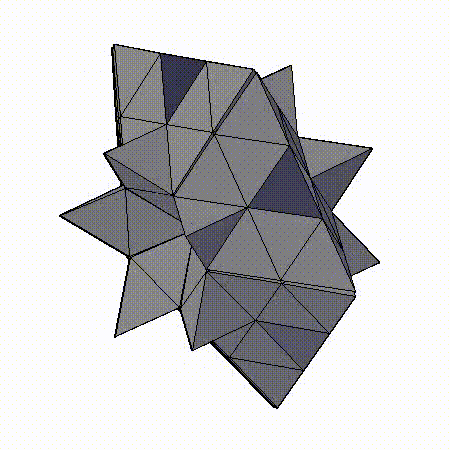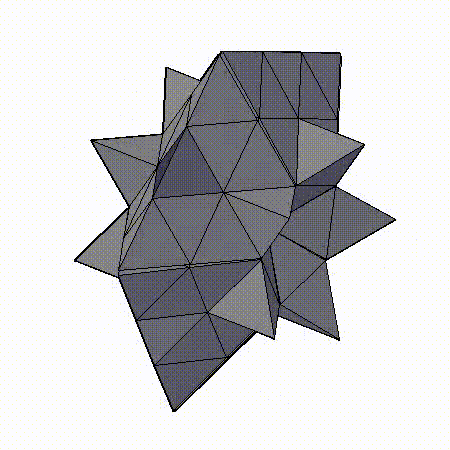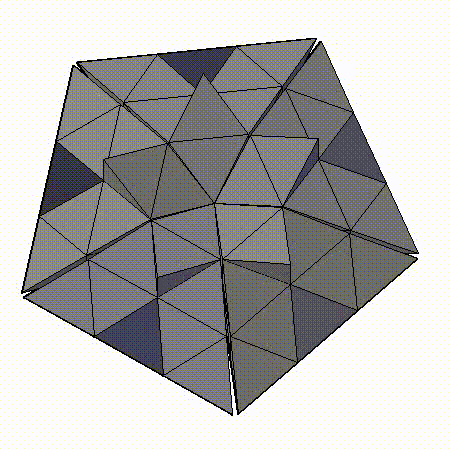
471-АТОМНЫЙ КЛАСТЕР С МОРФОЛОГИЕЙ ТРИАКОНТАЭДРА
С РАДИАЛЬНЫМ АЛГОРИТМОМ 1’(mm1’m)
J. Barker. The geometries of soft-sphere packings.
Journal de Physique Colloques, 1977, 38 (C2), pp.C2-37-C2-45.
381-АТОМНЫЙ КЛАСТЕР С РАДИАЛЬНЫМ АЛГОРИТМОМ 1’(m1’)p
J. Barker. THE GEOMETRIES OF SOFT-SPHERE PACKINGS.
Journal de Physique Colloques, 1977, 38 (C2), pp.C2-37-C2-45.
«МАЛЫЕ»
КЛАСТЕРЫ
МЕТАЛЛОВ
de Heer W.A. The physics of simple metal clusters: experimental aspects and simple models,
Rew. of Modern Physics, 1993, v.65, no.3, pp.611-676.
«СЛОЖНЫЕ» КЛАСТЕРЫ
МЕТАЛЛОВ
Бульенков Н.А. // «Вестник Нижегородского Университета им. Н.И. Лобачевского», серия «Физика твердого тела». 1998. вып.1. С.19.
- 471-АТОМНЫЙ КЛАСТЕР С МОРФОЛОГИЕЙ ТРИАКОНТАЭДРА С РАДИАЛЬНЫМ АЛГОРИТМОМ 1’(mm1’m)
- СИМПЛИЦИАЛЬНО-МОДУЛЬНЫЙ ДИЗАЙН 471-АТОМНОГО КЛАСТЕРА ИЗ D5h МОДУЛЕЙ
- 381-АТОМНЫЙ КЛАСТЕР С РАДИАЛЬНЫМ АЛГОРИТМОМ 1’(m1’)p
- «МАЛЫЕ» КЛАСТЕРЫ МЕТАЛЛОВ
- КЛАСТЕРЫ «СЛОЖНЫХ» СОЕДИНЕНИЙ
- КЛАСТЕРЫ ФУЛЛЕРЕНОВ
- МОДУЛЬНЫЙ ДИЗАЙН КЛАСТЕРА Pd145(COx)(PEt3)30
- ПОЛИЭДРИЧЕСКИЕ МОДЕЛИ КЛАСТЕРОВ С МАГИЧЕСКИМИ ЧИСЛАМИ АТОМОВ
- T-КЛАСТЕР НИКОЛАЯ АЛЕКСАНДРОВИЧА БУЛЬЕНКОВА
- КВАЗИКРИСТАЛЛЫ (МОДЕЛИ АППРОКСИМАНТОВ)