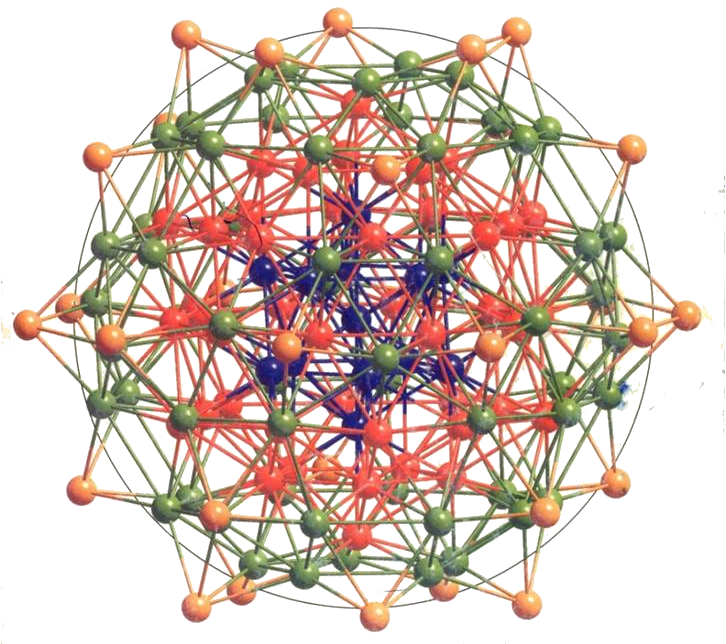
СИМПЛИЦИАЛЬНО-МОДУЛЬНОЕ ПРЕДСТАВЛЕНИЕ КЛАСТЕРА Pd145(COx)(PEt3)30, ПРЕДЛОЖЕННОЕ Н.А. БУЛЬЕНКОВЫМ
МОЛЕКУЛЯРНЫЙ ДИЗАЙН КЛАСТЕРА Pd14S(CO)X(PEt3)30, ПРЕДЛОЖЕННЫЙ АВТОРАМИ СТАТЬИ
Formal concentric construction of the capped three-shell nanosized Pd14S core of pseudo Ih symmetry in Pd14S(CO)x(PEt3)30:
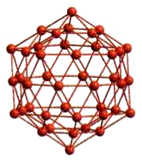
a) 12-atom ν1 icosahedron surrounding the central atom (νn denotes (n+1) equally spaced atoms along eachedge). This centrosymmetrically centered icosahedron, one o1 the live regular Platonic solids (with equivalent vertices and identical laces composed of only one polygon), comprises:
(1) six live-fold axes through opposite pairs of 12 vertices;
(2) 10 three-fold axes through midpoints of opposite pairs of 20 triangular faces; and
(3) 1S two-fold axes through midpoints of opposite pairs of 30 edges.

(a)
(b)

(c)
b) 42-atom ν2 icosahedron (shell 2) generated by the addition of an atom to the midpoint of each o1 the 30 edges o1 the 12-atom ν1 icosahedron.
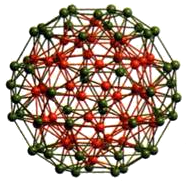
c) Shell 2 encapsulating the Pd- centered shell 1 to give a SS-atom Mackay icosahedron.
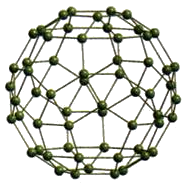
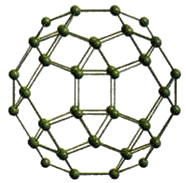
d) 60-atom polyhedron (shell 3), mathemati- cally named a rhombicosidodecahedron (3.4.S.4). The numbers N (in parentheses) designate the Schläfli symbol which represents in cyclic order the polygons (N-gons) meeting at each equivalent vertex.
(d)
(e)
e) Shell 3 encapsulating shell 2.
f) Another orientation of the outermost third-shell polyhedron that more clearly shows the 60 equivalent vertices along with the 62 faces (namely, the 12 pentagons, 20 equilateral triangles, and 30 squares). This Archimedean polyhedron, a semi-regular one in that all 60 vertices are identical but there are three different polygons, has pseudo Ih symmetry.
g) Entire 3-shell Pd14S core including 30 exopolyhedral Pd atoms (with attached triethylphosphane P atoms (purple)) that form square pyramids by capping of the 30 square polygons of the third shell.
(f)