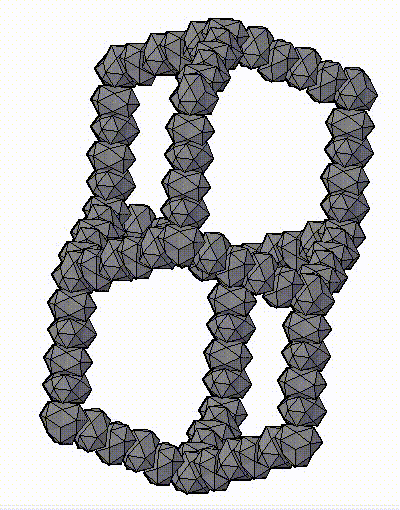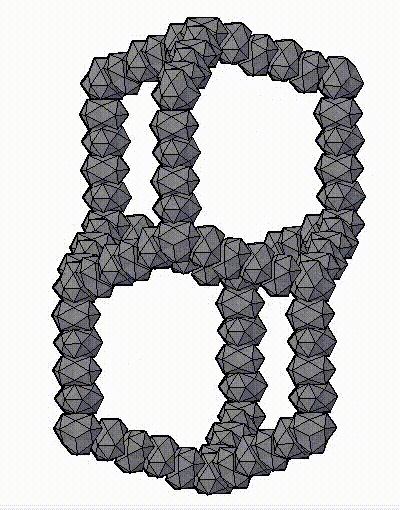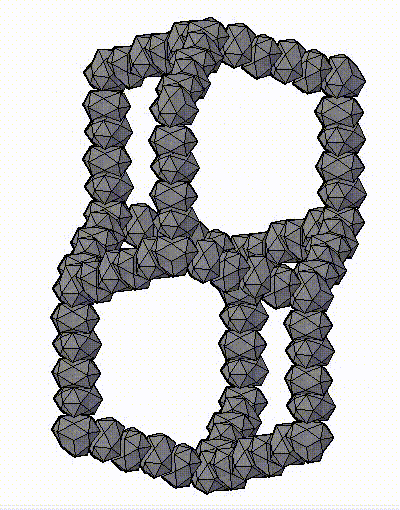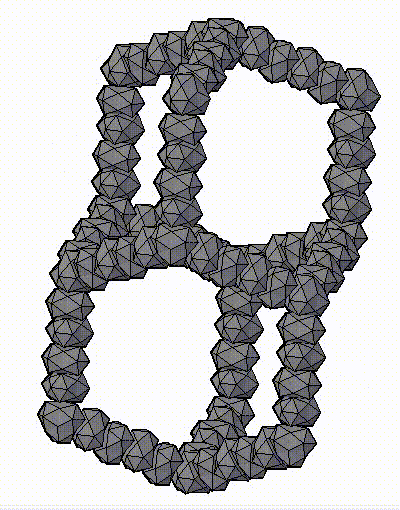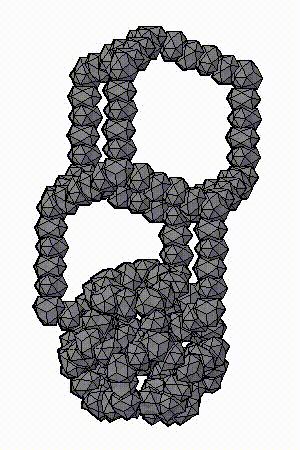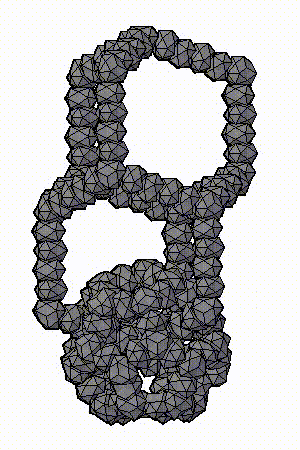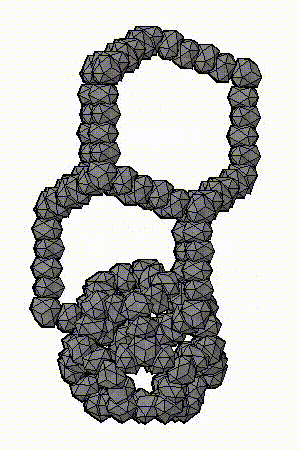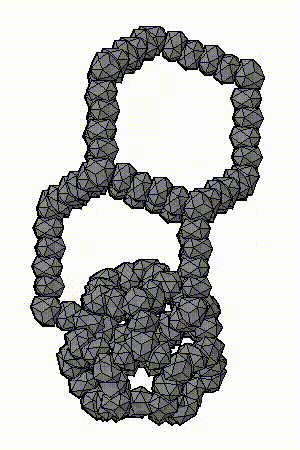КВАЗИКРИСТАЛЛЫ (МОДЕЛИ АППРОКСИМАНТОВ)
Основные работы
Бульенков Н.А., Крапошин В.С. (1993) Модульный подход к проблеме квазикристаллов. Письма в «Журнал технической физики», Т.19, №23, с.1-7.
Bulienkov NA, Phan Van An, Pham Van Nho (2003) Crystalline types of the approximants of 3-dimensional quasicrystals of various symmetries.
In: Proceedings of 48th international SAMPE symposium Advancing materials in the global economy – applications, emerging markets, and evolving technologies (May 2003). Long Beach. Book 1, pp 1191–1202.
МОДЕЛЬ АППРОКСИМАНТОВ КВАЗИКРИСТАЛЛОВ
Квазикристаллы были открыты Дэном Шехтманом 8 апреля 1982 года при анализе электронограммы быстрозатвердевших сплавов Al–Mn. Первый квазикристалл i-Al-Mn проявлял икосаэдрическую дифракционную симметрию и был отнесен к метастабильной фазе, как и все другие квазикристаллические фазы, полученные в последующем годы. В 1986 году был открыт первый стабильный икосаэдрический квазикристалл. система Al–Cu–Li [1].
Большинство квазикристаллов и аппроксимантов еще не охарактеризовано должным образом; редко известны их диапазон стабильности, симметрия и параметры решетки. В ряде случаев структуры уже решены дифракционными методами и дополнены электронно-микроскопическими исследованиями.
Модели аппроксимантов структуры внесли решающий вклад в понимание локальной структуры квазикристаллов. Обычная классификация квазикристаллических структур основана на кластерной модели их структуры. Применение моделей кластеров Маккея, псевдо-Маккея, Бергмана и ряда других показало, что это не очень надежная классификация [1].
Общей проблемой является лишь частичное «покрытие» моделью всех атомов структуры квазикристалла. Всегда остаются не охваченные моделью атомы – «атомы клея».
Н.А. Бульенков совершил огромный шаг в моделировании аппроксимантов квазикристаллов, когда в основу моделирования он положил принцип аналогичный организации структуры клатратных каркасов. Как известно, клатратные соединения разных типов формируют каркасы из полиэдров Аллена в определенной пропорции.
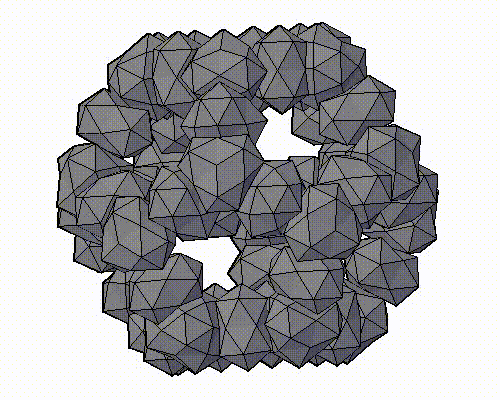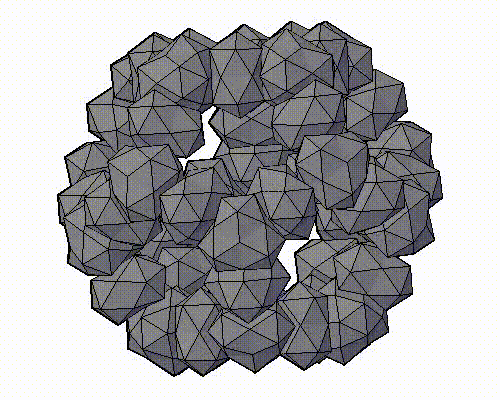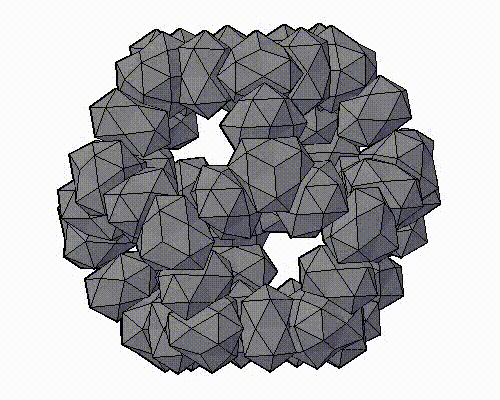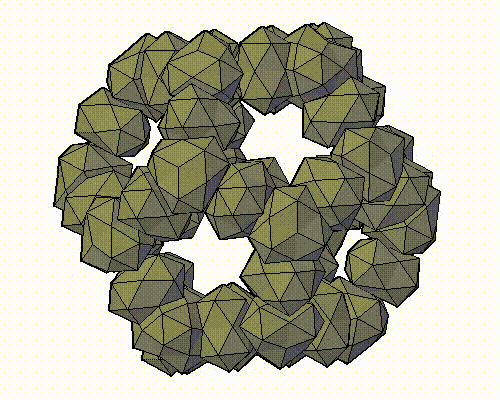
Модель аппроксимантов квазикристаллов, которую предложил Н.А. Бульенков является кластерно-стержневой.
На основе, разработанного им, метода модульного дизайна и использования в качестве «строительных блоков» кластеров из трех (симметрия D3h) и четырех (симметрия Td) взаимопроникающих икосаэдров. Тогда кластеры с симметрией Td формируют «вершины» полиэдров Аллена, а кластеры с симметрией D3h их «ребра». Пустоты в таком каркасе заполняются стержнями, также сформированными из этих кластеров-модулей («узлы» каркаса – кластеры с симметрией Td, «ребра» каркаса – кластеры с симметрией D3h), либо стержней из взаимопроникающих икосаэдров.
Библиография к материалу
1. W. Steurer, S. Deloudi Crystallography of Quasicrystals. Concepts, Methods and Structures. Springer Heidelberg Dordrecht London New York, 2009, 375 p.
ПРЕДСТАВЛЕНЫ ФРАГМЕНТЫ МОДЕЛЕЙ АППРОКСИМАНТОВ КВАЗИКРИСТАЛЛОВ, ПРЕДЛОЖЕННЫХ Н.А. БУЛЬЕНКОВЫМ